提供: Internet Web School

物理 ＞ 力学 ＞ 剛体と回転力

目次 1 剛体と回転力 1.1 　剛体の運動と回転 1.1.1 　剛体 1.1.2 　剛体の運動　 1.1.3 　固定軸のまわりの回転運動　 1.1.3.1 　回転運動の表示法　 1.2 　剛体に作用する力の回転力(トルク）　 1.2.1 　力と仕事の関係からの考察　 1.2.2 　剛体に力を加え微小角動かす時の、力のなす仕事の算出　 1.2.3 　ｚ軸まわりの回転力の導出　 1.2.4 　ｚ軸まわりの回転力（トルク）の性質 1.2.5 　他の軸の周りの回転力 1.2.6 　原点まわりの力のモーメント 1.2.7 　ベクトル積と回転による変位と力のモーメントのベクトル積表示 1.2.7.1 　ベクトル積にかんする命題　　　　 1.2.7.2 　軸周りの微小回転による変位のベクトル積表示　 1.2.7.3 　力のモーメントのベクトル積表示　　　 1.2.7.4 　2次元の場合のベクトル積 1.2.8 　力のモーメントの性質 1.2.8.1 　剛体の複数個所に作用する力の回転力とベクトル積表示　 1.2.8.1.1 　質点系に作用する重力のモーメント 1.3 　てこの原理と剛体の釣り合い 1.3.1 　てこの原理 1.3.2 　てこの原理の証明 1.3.3 　剛体の釣り合い

剛体と回転力

この節では、硬くて形を変えない質点系である剛体を回転させる力について考察する。

　剛体の運動と回転

　剛体

剛体(Rigid body)とは、
質点系であって、それらの、どの2質点の間の距離も変わらない,特殊な質点系のことを言う。
どの2質点の間の距離も変わらなければ変形は起こらない。
固くて変形しにくい物体を理想化した概念である。

　剛体の運動　

剛体は変形しない質点系なので、その運動は、重心の運動と、重心の周りの回転運動を合成したものになる。
重心の運動は前の節で説明したように、質点の運動と同じように簡単に扱える。
重心の周りの回転運動について解析するには、少し難しい数学が必要になる。

• ウィキペディア（剛体の力学）を参照のこと。

このテキストでは、固定軸の周りの回転運動を中心に、 剛体運動の初歩と釣合の条件について学ぶ。

　固定軸のまわりの回転運動　

剛体が、剛体の中を通る固定軸の周りを回転する運動（車輪の回転など）を考える。
応用も考え、回転軸は重心を通らなくてもよいように一般化しておく。
（注）なお、軸が動かないようにするためには軸受が必要である。
工夫しても回転時に軸は軸受から多少の摩擦力を受け、回転にブレーキがかかる。
しかし、これは無視出来るほど小さいと仮定する。
すると軸が受ける力は、軸の変動を防ぎ、固定軸の周りの運動に限定させる作用を持ち、
回転を遅める作用は持たないことになる。

　回転運動の表示法　

固定軸まわりの剛体の運動はどのように表示したらよいだろうか。
・剛体の位置を表す変数；回転角
剛体が幾ら回転したか分かるように、剛体の、回転軸上にない一点UNIQ39232c8b7e34f9b7-MathJax-449-QINUに印を付ける。
次に、角度を測る基準線をきめるため、座標系を決めよう。
UNIQ39232c8b7e34f9b7-MathJax-450-QINUから固定軸へ垂線をひき、その足を原点UNIQ39232c8b7e34f9b7-MathJax-451-QINUとし,固定軸をｚ座標とする(静止した)３次元直交座標UNIQ39232c8b7e34f9b7-MathJax-452-QINUを考える。
剛体が固定軸の周りを回転すると、印UNIQ39232c8b7e34f9b7-MathJax-453-QINUはxy平面上を、原点UNIQ39232c8b7e34f9b7-MathJax-454-QINUを中心に円を描いて動くことになる。
その位置ベクトルUNIQ39232c8b7e34f9b7-MathJax-455-QINUがx軸の正方向となす角度UNIQ39232c8b7e34f9b7-MathJax-456-QINUを、回転角と呼ぶ。図参照。
但し、x軸から反時計回りの角を正にする。
また一回転した後ならば、一回転の角UNIQ39232c8b7e34f9b7-MathJax-457-QINUを加え、逆周りに一回転した後ならUNIQ39232c8b7e34f9b7-MathJax-458-QINUを引き、
角度だけでなく回転数も分かるようにする。
回転角が指定されると、点UNIQ39232c8b7e34f9b7-MathJax-459-QINUの位置が決まる。
それだけでなく剛体は変形しないので、剛体のすべての点の位置がきまる。
そこで回転角UNIQ39232c8b7e34f9b7-MathJax-460-QINUの時間変化UNIQ39232c8b7e34f9b7-MathJax-461-QINUを明らかにすれば、剛体の回転運動は定まる。
固定軸のまわりの回転運動において回転角の果たし役割は、質点の運動において質点の位置が果たし役割に対応していることが分かる。
・回転の角速度と角加速度
UNIQ39232c8b7e34f9b7-MathJax-462-QINUを時間で微分したUNIQ39232c8b7e34f9b7-MathJax-463-QINUを回転の角速度と呼ぶ。
直観的には、時刻UNIQ39232c8b7e34f9b7-MathJax-464-QINUの瞬間の、回転の速さ（回転角の時間に対する変化率）を表す。
さらにもう一回時間微分したUNIQ39232c8b7e34f9b7-MathJax-465-QINUを回転の角加速度と呼ぶ。

　剛体に作用する力の回転力(トルク）　

質点の運動に倣って、剛体に作用する力によって、その位置(＝回転角）がどう変化するかの法則を導出したい。
しかし、剛体の回転の場合、ある方向の力は、剛体の回転に全く関係しない。 例えば、回転軸から放射状にでる半直線方向の力は全く回転の変化に寄与しない。
そこで剛体の回転を変化させる力とはなにかという問題から考察する必要が起こる。
質点運動における力の定義(力と運動量の変化の関係）や力と仕事の関係など力の係っている式のなかから、
剛体の回転運動に容易に拡張出来るものを選び、その式から、回転に関する力を求めることを試みる。
力の定義からは、回転運動への拡張を、推測することは難しい。
力と仕事の関係の考察をしてみよう。

　力と仕事の関係からの考察　

適当な直交座標系をさだめ、ベクトルは、座標成分で表示する。
質点に、一定の力UNIQ39232c8b7e34f9b7-MathJax-466-QINUを作用させて、x軸方向に変位させる。
質点はこの軸の上でしか動けないように拘束され、摩擦はないと仮定する。
質点の変位ベクトルは一次元の変数UNIQ39232c8b7e34f9b7-MathJax-467-QINUを使ってUNIQ39232c8b7e34f9b7-MathJax-468-QINUと表せる。
すると力のなす仕事は、UNIQ39232c8b7e34f9b7-MathJax-469-QINUである。　
逆に物体に一定の力を加え、x軸上でUNIQ39232c8b7e34f9b7-MathJax-470-QINUだけ変位させた時の仕事UNIQ39232c8b7e34f9b7-MathJax-471-QINUが分かれば、質点を動かした力は
UNIQ39232c8b7e34f9b7-MathJax-472-QINU
で求められる。
UNIQ39232c8b7e34f9b7-MathJax-473-QINUは、質点をx軸上で動かすことには全く寄与せず、
x軸に拘束された質点を動かす力は、UNIQ39232c8b7e34f9b7-MathJax-474-QINUなのである。
固定軸まわりの回転もその変位は一次元の変数である回転角度で表わせるので、
これに倣って、
UNIQ39232c8b7e34f9b7-MathJax-475-QINU回転した角度　
を、回転にかんする力であると考える。これを回転力と呼ぶ。トルクともいう。

この方針を実行して回転力を具体的に求めよう。

　剛体に力を加え微小角動かす時の、力のなす仕事の算出　

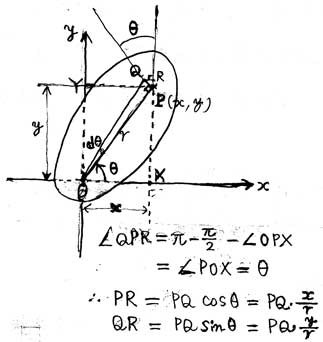
図4.1のように剛体の任意の一点UNIQ39232c8b7e34f9b7-MathJax-476-QINUを考える。
z座標の上方からxy平面を見下ろしているので、ｚ座標は点になりUNIQ39232c8b7e34f9b7-MathJax-477-QINUと書いてある。

まず一点UNIQ39232c8b7e34f9b7-MathJax-478-QINUに力UNIQ39232c8b7e34f9b7-MathJax-479-QINUが作用して、z座標軸を回転軸として微小角UNIQ39232c8b7e34f9b7-MathJax-480-QINUだけ回転したときの
仕事UNIQ39232c8b7e34f9b7-MathJax-481-QINUを計算し回転力を求めよう。
UNIQ39232c8b7e34f9b7-MathJax-482-QINU点から回転軸（ｚ軸）に垂線を下ろし、その足をUNIQ39232c8b7e34f9b7-MathJax-483-QINUとする。
UNIQ39232c8b7e34f9b7-MathJax-484-QINUの長さをUNIQ39232c8b7e34f9b7-MathJax-485-QINU、x軸となす角をUNIQ39232c8b7e34f9b7-MathJax-486-QINU(ラジアン)と置く。
この角度は、
剛体につけた印の位置ベクトルUNIQ39232c8b7e34f9b7-MathJax-487-QINUがｘ軸となす回転角UNIQ39232c8b7e34f9b7-MathJax-488-QINUと
このベクトルとUNIQ39232c8b7e34f9b7-MathJax-489-QINU（をｘｙ平面に平行移動したベクトル）の間の角の和である。
後者は、剛体なので、運動しても変わらない定数である。そこで、UNIQ39232c8b7e34f9b7-MathJax-490-QINU定数,と書ける。
剛体がｚ軸の周りを微小角UNIQ39232c8b7e34f9b7-MathJax-491-QINU回転して、点UNIQ39232c8b7e34f9b7-MathJax-492-QINUが図の点UNIQ39232c8b7e34f9b7-MathJax-493-QINUに移動したとする。
すると角UNIQ39232c8b7e34f9b7-MathJax-494-QINUはほぼ直角（=UNIQ39232c8b7e34f9b7-MathJax-495-QINU）でUNIQ39232c8b7e34f9b7-MathJax-496-QINUの長さUNIQ39232c8b7e34f9b7-MathJax-497-QINUは、UNIQ39232c8b7e34f9b7-MathJax-498-QINU。

UNIQ39232c8b7e34f9b7-MathJax-499-QINUのｘ成分とｙ成分は、図4－１中に示したように、それぞれ、UNIQ39232c8b7e34f9b7-MathJax-500-QINU、UNIQ39232c8b7e34f9b7-MathJax-501-QINU。
UNIQ39232c8b7e34f9b7-MathJax-502-QINUを代入すると、
UNIQ39232c8b7e34f9b7-MathJax-503-QINU、 UNIQ39232c8b7e34f9b7-MathJax-504-QINU、 UNIQ39232c8b7e34f9b7-MathJax-505-QINU
故に、
UNIQ39232c8b7e34f9b7-MathJax-506-QINU
点UNIQ39232c8b7e34f9b7-MathJax-507-QINUに作用する力UNIQ39232c8b7e34f9b7-MathJax-508-QINUが、物体をUNIQ39232c8b7e34f9b7-MathJax-509-QINUだけ動かしたので、
その仕事は、UNIQ39232c8b7e34f9b7-MathJax-510-QINU（内積）。
この右辺を内積の性質を用いて座標成分で表すと、
UNIQ39232c8b7e34f9b7-MathJax-511-QINU
UNIQ39232c8b7e34f9b7-MathJax-512-QINU

　ｚ軸まわりの回転力の導出　

ゆえに、力UNIQ39232c8b7e34f9b7-MathJax-513-QINUのｚ軸まわりの回転力（トルク）UNIQ39232c8b7e34f9b7-MathJax-514-QINUはUNIQ39232c8b7e34f9b7-MathJax-515-QINU に等しい。
これより、UNIQ39232c8b7e34f9b7-MathJax-516-QINUが得られる。
この式と、直線上に拘束された質点の運動における、力と仕事の関係式(　　節　　項）と対比させると、
UNIQ39232c8b7e34f9b7-MathJax-517-QINU　は、拘束された直線の上を動かすときに、働いた力の成分が対応し、
UNIQ39232c8b7e34f9b7-MathJax-518-QINU　は、変位量　　　に対応していることが分かる。

　ｚ軸まわりの回転力（トルク）の性質

(1)力UNIQ39232c8b7e34f9b7-MathJax-519-QINUのｚ軸まわりの回転力は,UNIQ39232c8b7e34f9b7-MathJax-520-QINUには関係しない。
言いかえるとz軸を固定軸とする剛体にｚ軸の方向の力を加えても、ｚ軸の周りの回転は起こらない。
(2)剛体の１点UNIQ39232c8b7e34f9b7-MathJax-521-QINUに作用する力UNIQ39232c8b7e34f9b7-MathJax-522-QINUを考える。
点UNIQ39232c8b7e34f9b7-MathJax-523-QINUからｚ軸に下ろした垂線の足をUNIQ39232c8b7e34f9b7-MathJax-524-QINUと書く。 力UNIQ39232c8b7e34f9b7-MathJax-525-QINUを、, UNIQ39232c8b7e34f9b7-MathJax-526-QINU方向の成分UNIQ39232c8b7e34f9b7-MathJax-527-QINUと、
ｚ軸まわりの回転によりUNIQ39232c8b7e34f9b7-MathJax-528-QINUの描く、UNIQ39232c8b7e34f9b7-MathJax-529-QINUを中心とする回転円の（左回りの）接線方向の成分UNIQ39232c8b7e34f9b7-MathJax-530-QINU
および、これら２成分に直交する成分(ｚ軸と平行)
に分解する(図参照）。この時、
・力UNIQ39232c8b7e34f9b7-MathJax-531-QINUのｚ軸まわりの回転力は、零である。
すなわち、動径方向の力は回転に寄与しない。　　
・力UNIQ39232c8b7e34f9b7-MathJax-532-QINUのｚ軸まわりの回転力は、UNIQ39232c8b7e34f9b7-MathJax-533-QINUのｚ軸まわりの回転力に等しい。
数式で表すと、UNIQ39232c8b7e34f9b7-MathJax-534-QINU
(3)剛体に作用する力の作用点を、力の作用線上で動かす限り、回転力は変化しない。
ここで、力の作用線とは、力の作用点を通り、力の方向と重なる直線のこと。

これらはいずれも直観と合致する。
証明は、試みてほしい。

　他の軸の周りの回転力

力UNIQ39232c8b7e34f9b7-MathJax-535-QINUのｘ軸、y軸まわりの回転力も同様に計算できる。結果は、
x軸まわりの回転力；UNIQ39232c8b7e34f9b7-MathJax-536-QINU
y軸まわりの回転力；UNIQ39232c8b7e34f9b7-MathJax-537-QINU

　原点まわりの力のモーメント

位置ベクトルUNIQ39232c8b7e34f9b7-MathJax-538-QINUの剛体の点UNIQ39232c8b7e34f9b7-MathJax-539-QINUに作用する力UNIQ39232c8b7e34f9b7-MathJax-540-QINUの原点まわりの力のモーメントを、
UNIQ39232c8b7e34f9b7-MathJax-541-QINUx軸まわりのトルク、y軸まわりのトルク、z軸まわりのトルクUNIQ39232c8b7e34f9b7-MathJax-542-QINUで定義する。
数式で書くと、
UNIQ39232c8b7e34f9b7-MathJax-543-QINU,

　ベクトル積と回転による変位と力のモーメントのベクトル積表示

以上の結果は、ベクトル積（vector product)を用いると簡潔、正確に表現でき、
回転運動の性質を調べるのが容易になる。

定義　ベクトル積
3次元ベクトルUNIQ39232c8b7e34f9b7-MathJax-544-QINU のベクトル積　UNIQ39232c8b7e34f9b7-MathJax-545-QINU　とは、
(1) 3次元ベクトルであり,
(2) 大きさは　UNIQ39232c8b7e34f9b7-MathJax-546-QINU を2辺とする平行四辺形の面積に等しい。
(3) 方向はこの四辺形に垂直で、向きは、UNIQ39232c8b7e34f9b7-MathJax-547-QINUが右手系をなすように定めたものである。
UNIQ39232c8b7e34f9b7-MathJax-548-QINU 　のなす角を　UNIQ39232c8b7e34f9b7-MathJax-549-QINU　とかくと、（２）の条件は、
UNIQ39232c8b7e34f9b7-MathJax-550-QINU
と書ける。

ベクトル積はクロス積あるいは外積とも呼ばれる。
ベクトル積に関して以下の8つの命題が成り立つ。

　ベクトル積にかんする命題　　　　

以下に述べる全ての命題で、
UNIQ39232c8b7e34f9b7-MathJax-551-QINUは3次元ベクトル
UNIQ39232c8b7e34f9b7-MathJax-552-QINUは実数とする。
命題１．
UNIQ39232c8b7e34f9b7-MathJax-553-QINU を, UNIQ39232c8b7e34f9b7-MathJax-554-QINUと垂直な成分UNIQ39232c8b7e34f9b7-MathJax-555-QINU と,平行な成分UNIQ39232c8b7e34f9b7-MathJax-556-QINU の和に分解するとき、
UNIQ39232c8b7e34f9b7-MathJax-557-QINU
UNIQ39232c8b7e34f9b7-MathJax-558-QINU

命題２．
UNIQ39232c8b7e34f9b7-MathJax-559-QINU

命題３
UNIQ39232c8b7e34f9b7-MathJax-560-QINU　

命題４．
UNIQ39232c8b7e34f9b7-MathJax-561-QINU　

命題４の系　　
　　 UNIQ39232c8b7e34f9b7-MathJax-562-QINU
UNIQ39232c8b7e34f9b7-MathJax-563-QINU

命題５．　
UNIQ39232c8b7e34f9b7-MathJax-564-QINU を
それぞれ大きさ(長さ)１で互いに直交し、右手系をなす、ベクトル(右手系をなす正規直交基底)とする。
この時、
UNIQ39232c8b7e34f9b7-MathJax-565-QINU
　

命題６．
ベクトルUNIQ39232c8b7e34f9b7-MathJax-566-QINUを,命題５で用いた基底UNIQ39232c8b7e34f9b7-MathJax-567-QINU で決まる座標の座標成分で表示しておく。
するとUNIQ39232c8b7e34f9b7-MathJax-568-QINU　

命題７．
UNIQ39232c8b7e34f9b7-MathJax-569-QINU

命題８．
UNIQ39232c8b7e34f9b7-MathJax-570-QINU と UNIQ39232c8b7e34f9b7-MathJax-571-QINUを,UNIQ39232c8b7e34f9b7-MathJax-572-QINUにかんして微分可能な、ベクトルに値をとる関数とする。すると、
UNIQ39232c8b7e34f9b7-MathJax-573-QINU は、UNIQ39232c8b7e34f9b7-MathJax-574-QINUにかんして微分可能で、
UNIQ39232c8b7e34f9b7-MathJax-575-QINU

これらの証明は、 物理数学の1.4節(ベクトル積)で扱う。
ベクトル積に関しては以下を参照のこと。

• ウィキペディア（ベクトル積　　）　

　軸周りの微小回転による変位のベクトル積表示　

補題
剛体がｚ軸の周りを微小角UNIQ39232c8b7e34f9b7-MathJax-576-QINU回転して、点UNIQ39232c8b7e34f9b7-MathJax-577-QINUがUNIQ39232c8b7e34f9b7-MathJax-578-QINUに移動したとする。
すると
UNIQ39232c8b7e34f9b7-MathJax-579-QINU
ここで、UNIQ39232c8b7e34f9b7-MathJax-580-QINU;点Pの位置ベクトル

何故ならば、
「剛体に力を加え微小角動かす時の、力のなす仕事の算出」の項の式（１）から、
UNIQ39232c8b7e34f9b7-MathJax-581-QINU
ベクトル積の定義から、所望の結果を得る。
同様にして、x軸まわりとｙ軸周りの微小回転による変位は、それぞれ、
UNIQ39232c8b7e34f9b7-MathJax-582-QINU、UNIQ39232c8b7e34f9b7-MathJax-583-QINU
で近似できる。

　力のモーメントのベクトル積表示　　　

ベクトル積の命題６を用いると、
位置ベクトルUNIQ39232c8b7e34f9b7-MathJax-584-QINUの点に作用するUNIQ39232c8b7e34f9b7-MathJax-585-QINU の
原点まわりの力のモーメントは、UNIQ39232c8b7e34f9b7-MathJax-586-QINU
x軸まわりの回転力(トルク）は、UNIQ39232c8b7e34f9b7-MathJax-587-QINU と表せることが分かる。
ｙ軸とｚ軸周りの回転力も、それぞれ　
UNIQ39232c8b7e34f9b7-MathJax-588-QINU ,UNIQ39232c8b7e34f9b7-MathJax-589-QINUで 表せる。

　2次元の場合のベクトル積

平面上の物体のＰ点に、平面内の力を作用させ、この平面内の一点Ｏの周りを回転させる問題を考える。
この平面にＯを原点とする2次元の直交右手座標をいれる。
力の作用点Ｐの位置ベクトルをUNIQ39232c8b7e34f9b7-MathJax-590-QINU、力をUNIQ39232c8b7e34f9b7-MathJax-591-QINUと座標表示する。
すでに説明したように、
Ｏ点周りの、力UNIQ39232c8b7e34f9b7-MathJax-592-QINUの回転力はUNIQ39232c8b7e34f9b7-MathJax-593-QINUである。
そこで、UNIQ39232c8b7e34f9b7-MathJax-594-QINUと定義する。
すると、 3次元のベクトル積の命題から
UNIQ39232c8b7e34f9b7-MathJax-595-QINU
という関係が成り立つことが分かる。
定義；2次元ベクトルのベクトル積
２つの2次元ベクトルUNIQ39232c8b7e34f9b7-MathJax-596-QINUのベクトル積UNIQ39232c8b7e34f9b7-MathJax-597-QINUとは、
UNIQ39232c8b7e34f9b7-MathJax-598-QINU
のことである。
3次元ベクトルの場合はベクトル積は再び3次元ベクトルになるが、2次元ベクトルのベクトル積は2次元でなく１次元であることが異なる。
しかし、2次元ベクトル積に対しても、3次元のベクトル積のもつ多くの性質が成り立つ。
命題；2次元ベクトル積の性質
任意の2次元ベクトルUNIQ39232c8b7e34f9b7-MathJax-599-QINUと
任意の実数UNIQ39232c8b7e34f9b7-MathJax-600-QINUに対して、以下の性質が成り立つ。
性質１．
UNIQ39232c8b7e34f9b7-MathJax-601-QINU を, UNIQ39232c8b7e34f9b7-MathJax-602-QINUと垂直な成分UNIQ39232c8b7e34f9b7-MathJax-603-QINU と,平行な成分UNIQ39232c8b7e34f9b7-MathJax-604-QINU の和に分解するとき、
UNIQ39232c8b7e34f9b7-MathJax-605-QINU
UNIQ39232c8b7e34f9b7-MathJax-606-QINU

性質２．
UNIQ39232c8b7e34f9b7-MathJax-607-QINU

性質３
UNIQ39232c8b7e34f9b7-MathJax-608-QINU　
性質４．
UNIQ39232c8b7e34f9b7-MathJax-609-QINU　

性質４の系　　
　　 UNIQ39232c8b7e34f9b7-MathJax-610-QINU
UNIQ39232c8b7e34f9b7-MathJax-611-QINU

性質５．　
UNIQ39232c8b7e34f9b7-MathJax-612-QINU を
それぞれ大きさ(長さ)１で互いに直交し、右手系をなす、ベクトル(右手系をなす正規直交基底)とする。
この時、
UNIQ39232c8b7e34f9b7-MathJax-613-QINU　
性質６．
UNIQ39232c8b7e34f9b7-MathJax-614-QINU と UNIQ39232c8b7e34f9b7-MathJax-615-QINUを,UNIQ39232c8b7e34f9b7-MathJax-616-QINUにかんして微分可能な、ベクトルに値をとる関数とする。すると、
UNIQ39232c8b7e34f9b7-MathJax-617-QINU は、UNIQ39232c8b7e34f9b7-MathJax-618-QINUにかんして微分可能で、
UNIQ39232c8b7e34f9b7-MathJax-619-QINU

　力のモーメントの性質

もっと一般に、どんな軸の周りの回転力も、UNIQ39232c8b7e34f9b7-MathJax-620-QINU　から得られる。
定理；
UNIQ39232c8b7e34f9b7-MathJax-621-QINUを、原点を始点とする大きさ１の任意のベクトルとする。
すると、
UNIQ39232c8b7e34f9b7-MathJax-622-QINU UNIQ39232c8b7e34f9b7-MathJax-623-QINUは、力UNIQ39232c8b7e34f9b7-MathJax-624-QINUのUNIQ39232c8b7e34f9b7-MathJax-625-QINU軸の周りの回転力になる。式で書くと、UNIQ39232c8b7e34f9b7-MathJax-626-QINU　
この式を、回転力の定義に基づいて言い換えると、
力UNIQ39232c8b7e34f9b7-MathJax-627-QINUのもとで、剛体をUNIQ39232c8b7e34f9b7-MathJax-628-QINU軸の右まわりに角度UNIQ39232c8b7e34f9b7-MathJax-629-QINUだけ回転させたとき、 UNIQ39232c8b7e34f9b7-MathJax-630-QINUのなす仕事UNIQ39232c8b7e34f9b7-MathJax-631-QINUは、UNIQ39232c8b7e34f9b7-MathJax-632-QINU
証明；
９つに分けて示す。
ⅰ）準備　
図のように、剛体の点　UNIQ39232c8b7e34f9b7-MathJax-633-QINU　から、UNIQ39232c8b7e34f9b7-MathJax-634-QINU　軸に垂線を下ろし、その足を　UNIQ39232c8b7e34f9b7-MathJax-635-QINU　とする。
力　UNIQ39232c8b7e34f9b7-MathJax-636-QINU　のもとで、剛体が　UNIQ39232c8b7e34f9b7-MathJax-637-QINU　を固定軸にして、
微小時間に、微小角UNIQ39232c8b7e34f9b7-MathJax-638-QINU だけ回転したとする。
このとき、UNIQ39232c8b7e34f9b7-MathJax-639-QINU　が移った先を、UNIQ39232c8b7e34f9b7-MathJax-640-QINU とする。
ⅱ）回転角　UNIQ39232c8b7e34f9b7-MathJax-641-QINU　が微小なので、
この回転中の　UNIQ39232c8b7e34f9b7-MathJax-642-QINU　の軌跡(円弧の微小部分）は、有向線分UNIQ39232c8b7e34f9b7-MathJax-643-QINU で精度高く、近似できる。
ⅲ）この間に力　UNIQ39232c8b7e34f9b7-MathJax-644-QINU　がなした仕事　UNIQ39232c8b7e34f9b7-MathJax-645-QINU　は、UNIQ39232c8b7e34f9b7-MathJax-646-QINU
この仕事を、回転角UNIQ39232c8b7e34f9b7-MathJax-647-QINUで割ると、力の　UNIQ39232c8b7e34f9b7-MathJax-648-QINU　軸周りの回転力が得られる。そこで、UNIQ39232c8b7e34f9b7-MathJax-649-QINU　を、この定理で与えられている諸量を使って表現し、これを用いて、仕事を計算しよう。
ⅳ）有向線分UNIQ39232c8b7e34f9b7-MathJax-650-QINUの方向を求める。
UNIQ39232c8b7e34f9b7-MathJax-651-QINU　は、UNIQ39232c8b7e34f9b7-MathJax-652-QINU　軸と垂直でUNIQ39232c8b7e34f9b7-MathJax-653-QINU　を通る平面UNIQ39232c8b7e34f9b7-MathJax-654-QINU上にあり、
UNIQ39232c8b7e34f9b7-MathJax-655-QINUを中心とする円の弧の微小部分をなすので、線分UNIQ39232c8b7e34f9b7-MathJax-656-QINU と直交する。UNIQ39232c8b7e34f9b7-MathJax-657-QINU
また、UNIQ39232c8b7e34f9b7-MathJax-658-QINU　軸と垂直でUNIQ39232c8b7e34f9b7-MathJax-659-QINU　を通る平面UNIQ39232c8b7e34f9b7-MathJax-660-QINU上にあるので、 UNIQ39232c8b7e34f9b7-MathJax-661-QINUはUNIQ39232c8b7e34f9b7-MathJax-662-QINU　軸とも直交し、従って線分UNIQ39232c8b7e34f9b7-MathJax-663-QINUと直交する。UNIQ39232c8b7e34f9b7-MathJax-664-QINU
ゆえに、UNIQ39232c8b7e34f9b7-MathJax-665-QINU　は、３点O,Q,Pを通る平面　UNIQ39232c8b7e34f9b7-MathJax-666-QINU　と直交する。
すると、UNIQ39232c8b7e34f9b7-MathJax-667-QINU　は、平面　UNIQ39232c8b7e34f9b7-MathJax-668-QINU　上のすべての線分と直交する。
ゆえに、UNIQ39232c8b7e34f9b7-MathJax-669-QINU,UNIQ39232c8b7e34f9b7-MathJax-670-QINU　
これで、UNIQ39232c8b7e34f9b7-MathJax-671-QINU　の方向は、求まった。
ⅴ）有向線分UNIQ39232c8b7e34f9b7-MathJax-672-QINU　の向き　
点　UNIQ39232c8b7e34f9b7-MathJax-673-QINU　は、UNIQ39232c8b7e34f9b7-MathJax-674-QINU　軸の周りを右周りに回転するので、その向きは、 UNIQ39232c8b7e34f9b7-MathJax-675-QINU と同じ向きである。
ⅵ）UNIQ39232c8b7e34f9b7-MathJax-676-QINU　の大きさ。
UNIQ39232c8b7e34f9b7-MathJax-677-QINUは、　UNIQ39232c8b7e34f9b7-MathJax-678-QINU　を中心とする、半径　UNIQ39232c8b7e34f9b7-MathJax-679-QINU の円弧の一部なので、 その中心角UNIQ39232c8b7e34f9b7-MathJax-680-QINU　を用いて、UNIQ39232c8b7e34f9b7-MathJax-681-QINU
ⅶ）ⅳ）、ⅴ）、ⅵ）から　 UNIQ39232c8b7e34f9b7-MathJax-682-QINU
ⅷ）UNIQ39232c8b7e34f9b7-MathJax-683-QINUが成り立つ。
なぜなら、
UNIQ39232c8b7e34f9b7-MathJax-684-QINU ,ここで　UNIQ39232c8b7e34f9b7-MathJax-685-QINU　はUNIQ39232c8b7e34f9b7-MathJax-686-QINU とUNIQ39232c8b7e34f9b7-MathJax-687-QINU　の間の角。
この式をⅶ)で得られた式に代入すれば、所望の結果が得られる。
ⅸ）UNIQ39232c8b7e34f9b7-MathJax-688-QINU
ⅹ）UNIQ39232c8b7e34f9b7-MathJax-689-QINU
定理の証明終わり。

（注）剛体が固定軸の周りでなく、自由に回転するときでも、
ある瞬間には、ある軸の周りの回転になっている。
力のモーメントは、どんな軸周りの回転力の情報も含んでいることが証明されたので、
　 回転運動一般に有効な概念であることが分かる。

　剛体の複数個所に作用する力の回転力とベクトル積表示　

次に剛体の多くの点に力を加えたときの回転力を求めよう。
力の作用点をUNIQ39232c8b7e34f9b7-MathJax-690-QINU、その位置ベクトルをUNIQ39232c8b7e34f9b7-MathJax-691-QINU、力をUNIQ39232c8b7e34f9b7-MathJax-692-QINUとする。
これらの力のもとで剛体がz軸まわりをUNIQ39232c8b7e34f9b7-MathJax-693-QINUだけ微小回転するときの、各力のなす仕事の合計は、
UNIQ39232c8b7e34f9b7-MathJax-694-QINU
従って、作用点UNIQ39232c8b7e34f9b7-MathJax-695-QINUの力UNIQ39232c8b7e34f9b7-MathJax-696-QINUの全体がもつz軸まわりの回転力は、
UNIQ39232c8b7e34f9b7-MathJax-697-QINU ここでUNIQ39232c8b7e34f9b7-MathJax-698-QINUは力UNIQ39232c8b7e34f9b7-MathJax-699-QINUのｚ軸まわりの回転力。

同様に、x軸まわりとy軸まわりの回転力も、それぞれ
UNIQ39232c8b7e34f9b7-MathJax-700-QINU
UNIQ39232c8b7e34f9b7-MathJax-701-QINU
力UNIQ39232c8b7e34f9b7-MathJax-702-QINUの原点周りに力のモーメントUNIQ39232c8b7e34f9b7-MathJax-703-QINUはUNIQ39232c8b7e34f9b7-MathJax-704-QINUで定義した。
全ての力の原点周りの力のモーメントも、同様に
UNIQ39232c8b7e34f9b7-MathJax-705-QINUで定義する。すると、
UNIQ39232c8b7e34f9b7-MathJax-706-QINU
全ての力の原点周りの力のモーメントUNIQ39232c8b7e34f9b7-MathJax-707-QINUも、上述の定理と同様の定理(定理の系と呼ぶ）が成り立つ。
定理の系
UNIQ39232c8b7e34f9b7-MathJax-708-QINUを剛体に作用する全ての力のモーメントとし、
UNIQ39232c8b7e34f9b7-MathJax-709-QINUを、原点を始点とする大きさ１の任意のベクトルとする。
すると、
UNIQ39232c8b7e34f9b7-MathJax-710-QINU UNIQ39232c8b7e34f9b7-MathJax-711-QINUは、力UNIQ39232c8b7e34f9b7-MathJax-712-QINUのUNIQ39232c8b7e34f9b7-MathJax-713-QINU軸の周りの回転力になる。
式で書くと、UNIQ39232c8b7e34f9b7-MathJax-714-QINU　
この式を、回転力の定義に基づいて言い換えると、
力UNIQ39232c8b7e34f9b7-MathJax-715-QINUのもとで、剛体をUNIQ39232c8b7e34f9b7-MathJax-716-QINU軸の右まわりに角度UNIQ39232c8b7e34f9b7-MathJax-717-QINUだけ回転させたとき、
これらの力のなす仕事UNIQ39232c8b7e34f9b7-MathJax-718-QINUは、UNIQ39232c8b7e34f9b7-MathJax-719-QINU

この系は、内積の性質を使えば、定理から、容易に導かれる。

　質点系に作用する重力のモーメント

質点に作用する重力を表示するため、次のような重力ベクトルUNIQ39232c8b7e34f9b7-MathJax-720-QINUを導入する。
UNIQ39232c8b7e34f9b7-MathJax-721-QINUの方向・向きは鉛直下方で 大きさは、UNIQ39232c8b7e34f9b7-MathJax-722-QINU(gは重力加速度)。
すると質量ｍの質点に作用する重力はUNIQ39232c8b7e34f9b7-MathJax-723-QINUで表せる。
ｎ個の質点系を考える。
空間の任意の点Ｏを原点に定める。
第ｉ質点の質量をUNIQ39232c8b7e34f9b7-MathJax-724-QINU、点Ｏから見た位置ベクトルをUNIQ39232c8b7e34f9b7-MathJax-725-QINUとする。
この質点系に作用する重力の原点周りのモーメントUNIQ39232c8b7e34f9b7-MathJax-726-QINUを求めよう。
命題　
質点系UNIQ39232c8b7e34f9b7-MathJax-727-QINUに作用する重力の原点周りのモーメントUNIQ39232c8b7e34f9b7-MathJax-728-QINUは、
その重心UNIQ39232c8b7e34f9b7-MathJax-729-QINUに全質量UNIQ39232c8b7e34f9b7-MathJax-730-QINUが集まったときの重力UNIQ39232c8b7e34f9b7-MathJax-731-QINUの原点周りのモーメントに等しい。
式で書くと、
UNIQ39232c8b7e34f9b7-MathJax-732-QINU
証明；
第ｉ質点に働く重力は、UNIQ39232c8b7e34f9b7-MathJax-733-QINU なので、
UNIQ39232c8b7e34f9b7-MathJax-734-QINU
UNIQ39232c8b7e34f9b7-MathJax-735-QINU
すでに学んだことから、この質点系の重心は、
UNIQ39232c8b7e34f9b7-MathJax-736-QINU
であった。ここで、 UNIQ39232c8b7e34f9b7-MathJax-737-QINU　。
これを用いて、モーメントを書きなおすと、
UNIQ39232c8b7e34f9b7-MathJax-738-QINU
となる。証明終わり。

　てこの原理と剛体の釣り合い

図のように剛体の棒の中間に支点UNIQ39232c8b7e34f9b7-MathJax-739-QINUがあり、
この点をとおり、図面に垂直な軸の周りを自由に回転する装置を梃子(てこ）と呼ぶ。
てこは、重いものをもちあげる道具として紀元前5000年ころから使われていた。

• ファイル:GENPHY00010206-00.jpg

  図　梃子（てこ）

　てこの原理

てこの棒の太さは、(長さに比べ非常に小さく)無視でき、
単位長さあたりの質量は一定で、UNIQ39232c8b7e34f9b7-MathJax-740-QINUとする。
このてこが
支点から距離UNIQ39232c8b7e34f9b7-MathJax-741-QINUにある棒の端UNIQ39232c8b7e34f9b7-MathJax-742-QINUに力UNIQ39232c8b7e34f9b7-MathJax-743-QINUを受け、
支点から距離UNIQ39232c8b7e34f9b7-MathJax-744-QINUにある反対側の端UNIQ39232c8b7e34f9b7-MathJax-745-QINUに力UNIQ39232c8b7e34f9b7-MathJax-746-QINUを受けて、
つりあっている(水平に静止し続ける)。

竿の両端UNIQ39232c8b7e34f9b7-MathJax-747-QINUを通り、UNIQ39232c8b7e34f9b7-MathJax-748-QINUからUNIQ39232c8b7e34f9b7-MathJax-749-QINUにむけた向きをつけた地面と水平な数直線をUNIQ39232c8b7e34f9b7-MathJax-750-QINU軸(x軸のこと)とし、
回転軸をUNIQ39232c8b7e34f9b7-MathJax-751-QINU軸(y軸のこと）にとり、支点Ｏを通る鉛直線に、下方に向かう向きをいれ、UNIQ39232c8b7e34f9b7-MathJax-752-QINU軸（ｚ軸のこと）にする。
UNIQ39232c8b7e34f9b7-MathJax-753-QINU軸(y軸)の向きは、直交座標系UNIQ39232c8b7e34f9b7-MathJax-754-QINUが右手系になるようにとる。図参照。
次の命題が成立する。
命題。てこの原理
UNIQ39232c8b7e34f9b7-MathJax-755-QINU
竿の重さを無視できるときは
UNIQ39232c8b7e34f9b7-MathJax-756-QINU
が成り立つ。
この式から、
もしUNIQ39232c8b7e34f9b7-MathJax-757-QINUならば、 UNIQ39232c8b7e34f9b7-MathJax-758-QINUに加える小さな力UNIQ39232c8b7e34f9b7-MathJax-759-QINUが、UNIQ39232c8b7e34f9b7-MathJax-760-QINUでは非常に大きな力UNIQ39232c8b7e34f9b7-MathJax-761-QINUになることが分かる。

• ウィキペディ（てこ）

も参照のこと。
経験から、てこの原理(式(2)）は相当昔から知られていたと思われる。
ギリシャ時代には、
アリストテレスや アルキメデスが、
この原理を述べ、論証を試みている。

アリストテレスは動力学的に論証したが、
当時の動力学は現代からみると間違いで、てこの原理の証明も誤っている。
アルキメデスは、
てこがつりあう条件の中から最も単純で直感的にも明らかと思われる性質をいくつか取り出し、
それらを正しいと仮定した。そしてこれらの性質だけを用いて梃子の原理を厳密に証明した。
現代でもこの方法で、てこの原理を証明する本が多い。
しかし、力学の基本法則以外の仮定が付加されるので、 本テキストではこの方法は採用しない。

　てこの原理の証明

今までの回転力の議論から、梃子がつりあっているときは、
UNIQ39232c8b7e34f9b7-MathJax-762-QINU(y)軸まわりの回転力が零であることが予想される。
このことをまづ論証する。
その準備のため、
剛体を膨大な個数Nの質点が互いに強固に結合した質点系と考える。
それらの質点に
以下に説明するように番号(i=0,1,2,,,N-1)をふり、第i番目の質点の質量をUNIQ39232c8b7e34f9b7-MathJax-763-QINU、位置ベクトルをUNIQ39232c8b7e34f9b7-MathJax-764-QINUとおく。
梃子がつりあっているときは、各質点は静止している。
ニュートンの第2法則と力の合成則により、
各質点に作用する外部力と内部力のベクトル和は零である。
（１）質点に働く外力
てこの両端UNIQ39232c8b7e34f9b7-MathJax-765-QINUと支点に作用する力と重力が外力となる。
点UNIQ39232c8b7e34f9b7-MathJax-766-QINUの質点に番号１をふり、その質量をUNIQ39232c8b7e34f9b7-MathJax-767-QINUと書く。
質点UNIQ39232c8b7e34f9b7-MathJax-768-QINUに力UNIQ39232c8b7e34f9b7-MathJax-769-QINUが作用する。
その位置ベクトルUNIQ39232c8b7e34f9b7-MathJax-770-QINUをUNIQ39232c8b7e34f9b7-MathJax-771-QINUと記す。
力UNIQ39232c8b7e34f9b7-MathJax-772-QINUが作用する質点をUNIQ39232c8b7e34f9b7-MathJax-773-QINUとおく。
その位置ベクトルをUNIQ39232c8b7e34f9b7-MathJax-774-QINUとする。
梃子の支点が梃子に及ぼす力UNIQ39232c8b7e34f9b7-MathJax-775-QINUが作用する質点をUNIQ39232c8b7e34f9b7-MathJax-776-QINUとする。
その位置ベクトルは、UNIQ39232c8b7e34f9b7-MathJax-777-QINUである。

その他の質点には、適当に番号(３からN-1まで）を振る。
質点UNIQ39232c8b7e34f9b7-MathJax-778-QINUの位置ベクトルをUNIQ39232c8b7e34f9b7-MathJax-779-QINUとおく。
また各質点UNIQ39232c8b7e34f9b7-MathJax-780-QINUに作用する重力はUNIQ39232c8b7e34f9b7-MathJax-781-QINUである。

（２）内部力
質点UNIQ39232c8b7e34f9b7-MathJax-782-QINUが、質点UNIQ39232c8b7e34f9b7-MathJax-783-QINUから受ける内部力をUNIQ39232c8b7e34f9b7-MathJax-784-QINUと書く。UNIQ39232c8b7e34f9b7-MathJax-785-QINU。
質点UNIQ39232c8b7e34f9b7-MathJax-786-QINUとUNIQ39232c8b7e34f9b7-MathJax-787-QINUの間の相互力にも作用・反作用の法則が成り立つので、UNIQ39232c8b7e34f9b7-MathJax-788-QINU。
さらに剛体では、その２質点間に働く力は、両質点を結ぶ直線の方向に働くと仮定してよい。言い換えるとUNIQ39232c8b7e34f9b7-MathJax-789-QINU。

（３）各質点に働く力の合力
各質点UNIQ39232c8b7e34f9b7-MathJax-790-QINUに作用する力の総和をUNIQ39232c8b7e34f9b7-MathJax-791-QINUと置くと、
次の式が成り立つ。
UNIQ39232c8b7e34f9b7-MathJax-792-QINU
UNIQ39232c8b7e34f9b7-MathJax-793-QINU
(4) 仮想仕事の原理
釣りあっている梃子に無限に小さい力を加え、
てこを回転軸(UNIQ39232c8b7e34f9b7-MathJax-794-QINU軸)まわりに微小角UNIQ39232c8b7e34f9b7-MathJax-795-QINU動かす時の
各質点の外力のなす仕事の総和は零である。

各質点の変位ベクトルをUNIQ39232c8b7e34f9b7-MathJax-796-QINUとかくと、
UNIQ39232c8b7e34f9b7-MathJax-797-QINU
UNIQ39232c8b7e34f9b7-MathJax-798-QINU
UNIQ39232c8b7e34f9b7-MathJax-799-QINU

ここで、UNIQ39232c8b7e34f9b7-MathJax-800-QINU
証明；
各質点に作用する合力UNIQ39232c8b7e34f9b7-MathJax-801-QINU　はすべて零ベクトルなので、
UNIQ39232c8b7e34f9b7-MathJax-802-QINU
合力を（３）に従って表現すると、
UNIQ39232c8b7e34f9b7-MathJax-803-QINU
なので、UNIQ39232c8b7e34f9b7-MathJax-804-QINUを示せば,式（５）の最初の等式が示せる。
UNIQ39232c8b7e34f9b7-MathJax-805-QINU軸まわりに微小角UNIQ39232c8b7e34f9b7-MathJax-806-QINU動かす時のてこの点P(位置ベクトルUNIQ39232c8b7e34f9b7-MathJax-807-QINU)の変位UNIQ39232c8b7e34f9b7-MathJax-808-QINUは「1.2.7.2 軸周りの微小回転による変位のベクトル積表示」の命題により、
UNIQ39232c8b7e34f9b7-MathJax-809-QINU
なので、
UNIQ39232c8b7e34f9b7-MathJax-810-QINU
UNIQ39232c8b7e34f9b7-MathJax-811-QINU
和をとるときに使う変数は、どの変数名を使っても、和は同じになるので、
上式の括弧(　）内の第2項の変数名UNIQ39232c8b7e34f9b7-MathJax-812-QINUを UNIQ39232c8b7e34f9b7-MathJax-813-QINUに置き換えると、
UNIQ39232c8b7e34f9b7-MathJax-814-QINU
UNIQ39232c8b7e34f9b7-MathJax-815-QINU
内部力が作用反作用の法則を満たすことから
UNIQ39232c8b7e34f9b7-MathJax-816-QINU
内積とベクトル積のスカラー倍の性質を使って変形すると、
UNIQ39232c8b7e34f9b7-MathJax-817-QINU
変数 i'、 j' を変数 i、j に変えると
UNIQ39232c8b7e34f9b7-MathJax-818-QINU
故に
UNIQ39232c8b7e34f9b7-MathJax-819-QINU

この式を式（6）に代入し、内積とベクトル積の性質を使って整頓すると、
UNIQ39232c8b7e34f9b7-MathJax-820-QINU
ベクトル積の命題７から、
UNIQ39232c8b7e34f9b7-MathJax-821-QINU
UNIQ39232c8b7e34f9b7-MathJax-822-QINUなので
UNIQ39232c8b7e34f9b7-MathJax-823-QINU
故に、
UNIQ39232c8b7e34f9b7-MathJax-824-QINU
所望の結果がえられたので、式(5)の最初の等式
UNIQ39232c8b7e34f9b7-MathJax-825-QINUが証明できた。

UNIQ39232c8b7e34f9b7-MathJax-826-QINUを代入すると
UNIQ39232c8b7e34f9b7-MathJax-827-QINU
が得られる。
さらに、内積とベクトル積の性質を使い、変形すると
UNIQ39232c8b7e34f9b7-MathJax-828-QINU
これで式（５）をすべて示した。仮想仕事の原理の証明終わり。
(注1）ここまでの議論は、梃子の形状や各質点に働く外力UNIQ39232c8b7e34f9b7-MathJax-829-QINUという仮定は、全く使用していない。
従ってこの命題は任意の剛体で成り立つ。
(注２）静止している剛体では、UNIQ39232c8b7e34f9b7-MathJax-830-QINUであることが、仮想仕事の原理を使わず、直接証明できる。後述する。

(5)てこの原理 の証明

仮想仕事の原理から
UNIQ39232c8b7e34f9b7-MathJax-831-QINU
内積とベクトル積の性質を利用して
UNIQ39232c8b7e34f9b7-MathJax-832-QINU
この式にUNIQ39232c8b7e34f9b7-MathJax-833-QINUを 代入し変形すると
UNIQ39232c8b7e34f9b7-MathJax-834-QINU 故に、 UNIQ39232c8b7e34f9b7-MathJax-835-QINU
上式の第２項を、ベクトル積の性質７を用いて変形すると、
UNIQ39232c8b7e34f9b7-MathJax-836-QINU
UNIQ39232c8b7e34f9b7-MathJax-837-QINU
これを式（７）も右辺に代入すると UNIQ39232c8b7e34f9b7-MathJax-838-QINU
上式の第２項の和 UNIQ39232c8b7e34f9b7-MathJax-839-QINU を、
支点からみて、
UNIQ39232c8b7e34f9b7-MathJax-840-QINU側の質点についての和UNIQ39232c8b7e34f9b7-MathJax-841-QINUと、
UNIQ39232c8b7e34f9b7-MathJax-842-QINU側の質点についての和UNIQ39232c8b7e34f9b7-MathJax-843-QINUと 真上にある質点についての和　UNIQ39232c8b7e34f9b7-MathJax-844-QINU　に分ける。
すると、
UNIQ39232c8b7e34f9b7-MathJax-845-QINU
この右辺の第１項は、支点からみて梃子のUNIQ39232c8b7e34f9b7-MathJax-846-QINU側の部分の質量UNIQ39232c8b7e34f9b7-MathJax-847-QINUと
その部分の重心 UNIQ39232c8b7e34f9b7-MathJax-848-QINUを用いて
UNIQ39232c8b7e34f9b7-MathJax-849-QINU
同様に、第２項は、支点からみて梃子のUNIQ39232c8b7e34f9b7-MathJax-850-QINU側の部分の質量UNIQ39232c8b7e34f9b7-MathJax-851-QINUと
その部分の重心UNIQ39232c8b7e34f9b7-MathJax-852-QINU　を用いて、
UNIQ39232c8b7e34f9b7-MathJax-853-QINU
となる。梃子の真上の部分の質量は無視できるので、第3項は０としてよい。
故に
UNIQ39232c8b7e34f9b7-MathJax-854-QINU
この式を式（８）に代入すると、
UNIQ39232c8b7e34f9b7-MathJax-855-QINU
UNIQ39232c8b7e34f9b7-MathJax-856-QINU　側の部分を左辺に移行すると、 UNIQ39232c8b7e34f9b7-MathJax-857-QINU
これまでは
天秤の棒の条件（太さは無視でき、単位長さ当たりの質量は一定でUNIQ39232c8b7e34f9b7-MathJax-858-QINU）
を使わず議論してきたが、ここでこの条件を使う。
すると、
UNIQ39232c8b7e34f9b7-MathJax-859-QINU
UNIQ39232c8b7e34f9b7-MathJax-860-QINU
UNIQ39232c8b7e34f9b7-MathJax-861-QINU
ここで均質な棒の重心はその中点になる事実を用いた。
これらを式（９）に代入して、ベクトル積と内積の計算を実行すると、
UNIQ39232c8b7e34f9b7-MathJax-862-QINU
を得る。
梃子の原理の証明終わり。

　剛体の釣り合い

剛体は、静止しているか、等速度で並進運動しているとき、釣り合っているという。
剛体を膨大な数の質点UNIQ39232c8b7e34f9b7-MathJax-863-QINUが、強固に結合した質点系と考えると、
釣り合い条件とは、
すべての質点が静止しているか、すべての質点が同じ速度で直線運動していることを意味する。
この時次の命題が成立する。
命題 剛体の釣り合いの必要条件
剛体がつりあっているならば、剛体に作用するすべての外力のベクトル和は零で、
剛体に作用するすべての外力の、任意の点の周りの力のモーメントは零である。
この条件を式で書こう。
剛体を質点系UNIQ39232c8b7e34f9b7-MathJax-864-QINUとみなし、
各質点UNIQ39232c8b7e34f9b7-MathJax-865-QINUの位置ベクトルをUNIQ39232c8b7e34f9b7-MathJax-866-QINU、
それに作用する外力の合力をUNIQ39232c8b7e34f9b7-MathJax-867-QINUとすると、
UNIQ39232c8b7e34f9b7-MathJax-868-QINU
UNIQ39232c8b7e34f9b7-MathJax-869-QINU
証明
剛体の各質点は静止(あるいは全てが等速直線運動）しているので、
各質点UNIQ39232c8b7e34f9b7-MathJax-870-QINUに作用する力の合力UNIQ39232c8b7e34f9b7-MathJax-871-QINUは零でなければならない。
式（１０）を示そう。
UNIQ39232c8b7e34f9b7-MathJax-872-QINU
UNIQ39232c8b7e34f9b7-MathJax-873-QINUを代入すると、
UNIQ39232c8b7e34f9b7-MathJax-874-QINU
UNIQ39232c8b7e34f9b7-MathJax-875-QINU
作用・反作用の法則によりUNIQ39232c8b7e34f9b7-MathJax-876-QINUなので、
UNIQ39232c8b7e34f9b7-MathJax-877-QINU
式（１０）が証明できた。
式（１１）をしめそう。
UNIQ39232c8b7e34f9b7-MathJax-878-QINU
すると、
UNIQ39232c8b7e34f9b7-MathJax-879-QINU
UNIQ39232c8b7e34f9b7-MathJax-880-QINUを代入して、ベクトル積の性質を使うと、
UNIQ39232c8b7e34f9b7-MathJax-881-QINU
UNIQ39232c8b7e34f9b7-MathJax-882-QINU
この式の第2項が零であれば、UNIQ39232c8b7e34f9b7-MathJax-883-QINU が証明される。
すでに前節で示したように、
UNIQ39232c8b7e34f9b7-MathJax-884-QINU
UNIQ39232c8b7e34f9b7-MathJax-885-QINU
UNIQ39232c8b7e34f9b7-MathJax-886-QINUを第２項に代入すると、
UNIQ39232c8b7e34f9b7-MathJax-887-QINU
UNIQ39232c8b7e34f9b7-MathJax-888-QINUなので、ベクトル積の性質から、
UNIQ39232c8b7e34f9b7-MathJax-889-QINU
故にUNIQ39232c8b7e34f9b7-MathJax-890-QINU　が示せた。
命題の証明終わり。
次節(2.6 剛体の回転運動と釣合い）で、この命題の逆も正しいことを示す。
命題の系
命題において、質点UNIQ39232c8b7e34f9b7-MathJax-891-QINUに作用する外力が、重力とその他の力の和
UNIQ39232c8b7e34f9b7-MathJax-892-QINUで表せるとき
剛体の釣合の条件は
UNIQ39232c8b7e34f9b7-MathJax-893-QINU、
UNIQ39232c8b7e34f9b7-MathJax-894-QINU
である。
証明は簡単なので省略する。