拘束のある問題
提供: Internet Web School
目次 |
等式拘束のある問題
陰関数定理とラグランジュ乗数
以下の問題を考える.
UNIQ24238028548781d1-MathJax-173-QINUとするとき,
半径1の円周
UNIQ24238028548781d1-MathJax-174-QINU
上の点UNIQ24238028548781d1-MathJax-175-QINUでUNIQ24238028548781d1-MathJax-176-QINUの最大にするものを求めよ.
関数の極値条件
実数値関数UNIQ24238028548781d1-MathJax-177-QINUがUNIQ24238028548781d1-MathJax-178-QINUで極小値または極大値をとり,かつ,UNIQ24238028548781d1-MathJax-179-QINUで微分可能であれば,
UNIQ24238028548781d1-MathJax-180-QINUのUNIQ24238028548781d1-MathJax-181-QINUでの微分係数はUNIQ24238028548781d1-MathJax-182-QINUである。
UNIQ24238028548781d1-MathJax-183-QINU
陰関数
半径1の円の方程式
UNIQ24238028548781d1-MathJax-184-QINU
に注目する。判りやすいように,
UNIQ24238028548781d1-MathJax-185-QINU としておく.
UNIQ24238028548781d1-MathJax-186-QINU とすると, UNIQ24238028548781d1-MathJax-187-QINUではUNIQ24238028548781d1-MathJax-188-QINUの方程式を満たすUNIQ24238028548781d1-MathJax-189-QINUについては UNIQ24238028548781d1-MathJax-190-QINU という関係が成り立っている.
このUNIQ24238028548781d1-MathJax-191-QINUという関数は,UNIQ24238028548781d1-MathJax-192-QINU式の中には出てこない.UNIQ24238028548781d1-MathJax-193-QINUからこのように間接的に導き出される関数を陰関数と呼ぶ.
一般化すれば特定の条件のもとに
UNIQ24238028548781d1-MathJax-194-QINUという式から陰関数UNIQ24238028548781d1-MathJax-195-QINUが定義される。
上の例では UNIQ24238028548781d1-MathJax-196-QINU
しかし,何時でも上の例のように,UNIQ24238028548781d1-MathJax-197-QINUから陰関数UNIQ24238028548781d1-MathJax-198-QINUが定義されるわけではない.
陰関数定理
ある領域DUNIQ24238028548781d1-MathJax-199-QINUで関数UNIQ24238028548781d1-MathJax-200-QINUが連続でかつ,UNIQ24238028548781d1-MathJax-201-QINUについて偏微分可能で, その偏導関数
UNIQ24238028548781d1-MathJax-202-QINU
UNIQ24238028548781d1-MathJax-203-QINU
もUNIQ24238028548781d1-MathJax-204-QINUについて連続とする。
D内の1点UNIQ24238028548781d1-MathJax-205-QINUで
UNIQ24238028548781d1-MathJax-206-QINU
であり,
UNIQ24238028548781d1-MathJax-207-QINU
とする. このとき,UNIQ24238028548781d1-MathJax-208-QINUを含む開区間UNIQ24238028548781d1-MathJax-209-QINUとその上の連続関数UNIQ24238028548781d1-MathJax-210-QINUが存在し,
1) 開区間UNIQ24238028548781d1-MathJax-211-QINU上でUNIQ24238028548781d1-MathJax-212-QINU
2) UNIQ24238028548781d1-MathJax-213-QINU
3) 開区間UNIQ24238028548781d1-MathJax-214-QINU上で,
UNIQ24238028548781d1-MathJax-215-QINU
上の定理でUNIQ24238028548781d1-MathJax-216-QINUの役目を反対にすれば,UNIQ24238028548781d1-MathJax-217-QINU となる陰関数の存在が示される.
ラグランジュ乗数法
関数UNIQ24238028548781d1-MathJax-218-QINUが,制約条件 UNIQ24238028548781d1-MathJax-219-QINU の元にUNIQ24238028548781d1-MathJax-220-QINUで極値(極大値か極小値)をとるとする。
UNIQ24238028548781d1-MathJax-221-QINUがUNIQ24238028548781d1-MathJax-222-QINUについて微分可能な関数で, 関数UNIQ24238028548781d1-MathJax-223-QINUはUNIQ24238028548781d1-MathJax-224-QINUが上の陰関数定理を適用できる条件を満たしているものとする。 UNIQ24238028548781d1-MathJax-225-QINUの近傍で関数UNIQ24238028548781d1-MathJax-226-QINUが存在して,UNIQ24238028548781d1-MathJax-227-QINUのその近傍では UNIQ24238028548781d1-MathJax-228-QINU が成り立ち,UNIQ24238028548781d1-MathJax-229-QINU,UNIQ24238028548781d1-MathJax-230-QINUも成り立っている. UNIQ24238028548781d1-MathJax-231-QINUの役目を反対にすれば,UNIQ24238028548781d1-MathJax-232-QINU となる陰関数を用いることになるが議論は全く同様に できる.
関数UNIQ24238028548781d1-MathJax-233-QINUはUNIQ24238028548781d1-MathJax-234-QINUで極値(極大値か極小値)をとるから
UNIQ24238028548781d1-MathJax-235-QINUもUNIQ24238028548781d1-MathJax-236-QINUで極値を取る.
極値条件により
UNIQ24238028548781d1-MathJax-237-QINU
である.
このUNIQ24238028548781d1-MathJax-238-QINUについての微分を求めるとUNIQ24238028548781d1-MathJax-239-QINUは合成関数であるから
UNIQ24238028548781d1-MathJax-240-QINU
UNIQ24238028548781d1-MathJax-241-QINUであるからUNIQ24238028548781d1-MathJax-242-QINU式を上のUNIQ24238028548781d1-MathJax-243-QINU式に代入し
UNIQ24238028548781d1-MathJax-244-QINU
という変数を使うと,
UNIQ24238028548781d1-MathJax-245-QINU
また
UNIQ24238028548781d1-MathJax-246-QINU
から
UNIQ24238028548781d1-MathJax-247-QINU
すなわちUNIQ24238028548781d1-MathJax-248-QINUという新しい変数を使って
UNIQ24238028548781d1-MathJax-249-QINU
という関数を造ると:
関数UNIQ24238028548781d1-MathJax-250-QINUが制約条件UNIQ24238028548781d1-MathJax-251-QINU を充たすという条件の下に UNIQ24238028548781d1-MathJax-252-QINUで極値(極大値か極小値)をとる という条件からUNIQ24238028548781d1-MathJax-253-QINUについての制約のない場合の極値条件
UNIQ24238028548781d1-MathJax-254-QINU
が導かれる.制約条件付きの極値問題から,UNIQ24238028548781d1-MathJax-255-QINUという人工的な変数を使って
UNIQ24238028548781d1-MathJax-256-QINU の制約条件のない場合の極値条件が導かれる.
ただしこの議論は「その点が最大(小)値を与える」UNIQ24238028548781d1-MathJax-257-QINU 「その点が極値を与える」UNIQ24238028548781d1-MathJax-258-QINU 「その点でのUNIQ24238028548781d1-MathJax-259-QINU」
という必要条件の連鎖であるので注意が必要である.
「UNIQ24238028548781d1-MathJax-260-QINU」は必要条件であるから, これが満たされても,極値かどうかチェックの必要があり,さらにはUNIQ24238028548781d1-MathJax-261-QINUの極値を与えるUNIQ24238028548781d1-MathJax-262-QINUが求められたとしても, それが最大(小)値を与えるのか確かめる必要がある。
また,少なくともUNIQ24238028548781d1-MathJax-263-QINUとUNIQ24238028548781d1-MathJax-264-QINUがUNIQ24238028548781d1-MathJax-265-QINUについて微分可能であることも必要である.
ここで使われたUNIQ24238028548781d1-MathJax-266-QINUはラグランジュ乗数と呼ばれる. 上の問題に適用すると
UNIQ24238028548781d1-MathJax-267-QINU
拘束条件UNIQ24238028548781d1-MathJax-268-QINU を充たし,UNIQ24238028548781d1-MathJax-269-QINUの極値を与える UNIQ24238028548781d1-MathJax-270-QINUが存在すると仮定すれば,
UNIQ24238028548781d1-MathJax-271-QINU または UNIQ24238028548781d1-MathJax-272-QINU であり,
陰関数の存在条件 UNIQ24238028548781d1-MathJax-273-QINU または UNIQ24238028548781d1-MathJax-274-QINU が成り立っている.
そこで,
UNIQ24238028548781d1-MathJax-275-QINU
とおけば
UNIQ24238028548781d1-MathJax-276-QINU
UNIQ24238028548781d1-MathJax-277-QINU式から UNIQ24238028548781d1-MathJax-278-QINU であり,
UNIQ24238028548781d1-MathJax-279-QINU式から
UNIQ24238028548781d1-MathJax-280-QINU
これをUNIQ24238028548781d1-MathJax-281-QINU 式に代入して
UNIQ24238028548781d1-MathJax-282-QINU
よって
UNIQ24238028548781d1-MathJax-283-QINU または UNIQ24238028548781d1-MathJax-284-QINU
UNIQ24238028548781d1-MathJax-285-QINU のときUNIQ24238028548781d1-MathJax-286-QINU であり,UNIQ24238028548781d1-MathJax-287-QINU
UNIQ24238028548781d1-MathJax-288-QINU のときUNIQ24238028548781d1-MathJax-289-QINU であり,UNIQ24238028548781d1-MathJax-290-QINU
従って
等式拘束条件
UNIQ24238028548781d1-MathJax-291-QINU
の下でUNIQ24238028548781d1-MathJax-292-QINU の
最大値はUNIQ24238028548781d1-MathJax-293-QINUのときでUNIQ24238028548781d1-MathJax-294-QINU
Microsoft Excel のソルバーで解くこともできる.
データの入力とソルバーのパラメータは以下の通りである.解析には非線形問題を選択する.
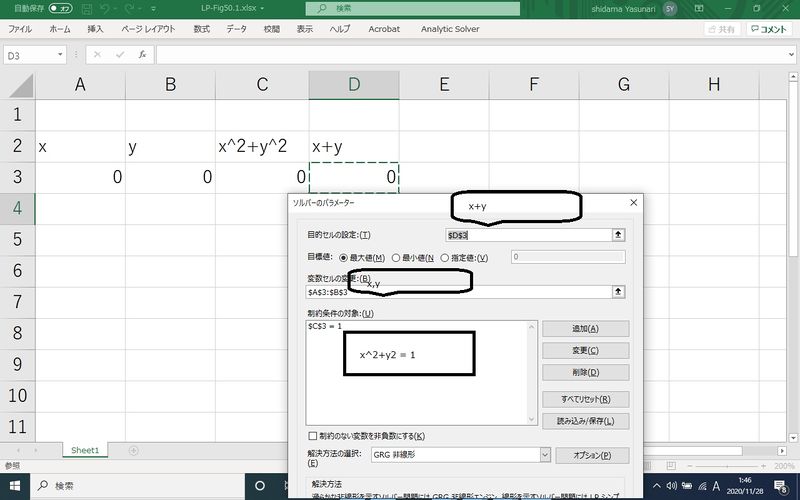
ソルバーの出力は以下の通りであり前期の解析解と同じである.
上記の議論を一般化したものが以下である.
UNIQ24238028548781d1-MathJax-295-QINU
がUNIQ24238028548781d1-MathJax-296-QINUでUNIQ24238028548781d1-MathJax-297-QINU個の制約条件
UNIQ24238028548781d1-MathJax-298-QINU
のもとでの極少(極大)値をとるものとする.さらにUNIQ24238028548781d1-MathJax-299-QINU個のUNIQ24238028548781d1-MathJax-300-QINU次元 ベクトル
UNIQ24238028548781d1-MathJax-301-QINU
が一次独立とする.これは前項のUNIQ24238028548781d1-MathJax-302-QINU式の陰関数の存在条件 UNIQ24238028548781d1-MathJax-303-QINU に相当する.
UNIQ24238028548781d1-MathJax-304-QINU個のUNIQ24238028548781d1-MathJax-305-QINU次元 ベクトルからなるUNIQ24238028548781d1-MathJax-306-QINU行列 UNIQ24238028548781d1-MathJax-307-QINU の階数がUNIQ24238028548781d1-MathJax-308-QINU であることと同値である.
このとき,一変数関数の場合と同様,以下が成立つ.すなわち, UNIQ24238028548781d1-MathJax-309-QINU次元のラグランジュ乗数ベクトル
UNIQ24238028548781d1-MathJax-310-QINU が存在し,
UNIQ24238028548781d1-MathJax-311-QINU
はUNIQ24238028548781d1-MathJax-312-QINUで停留条件を充す.
すなわち
UNIQ24238028548781d1-MathJax-313-QINU
が成りたつ.
不等式拘束のある問題
前項では,等式拘束問題を扱った.この項では不等式拘束問題を扱う. 先ず,UNIQ24238028548781d1-MathJax-314-QINUの部分集合
UNIQ24238028548781d1-MathJax-315-QINU
を定義しておく.この(正錐)UNIQ24238028548781d1-MathJax-316-QINUを使って,UNIQ24238028548781d1-MathJax-317-QINUの 順序(大小)を
UNIQ24238028548781d1-MathJax-318-QINU
で定義する.
UNIQ24238028548781d1-MathJax-319-QINUからUNIQ24238028548781d1-MathJax-320-QINUへの微分可能な写像
UNIQ24238028548781d1-MathJax-321-QINU で定義されるものとする.
不等式制約
UNIQ24238028548781d1-MathJax-322-QINU
について,この項では以下のクーン・タッカーの条件が成立つものとする.
クーン・タッカーの条件
UNIQ24238028548781d1-MathJax-323-QINU を充たす任意のUNIQ24238028548781d1-MathJax-324-QINUについて
UNIQ24238028548781d1-MathJax-325-QINU
となる UNIQ24238028548781d1-MathJax-326-QINUが存在する.
ただし,
UNIQ24238028548781d1-MathJax-327-QINU
ここで, UNIQ24238028548781d1-MathJax-328-QINU は順序(大小関係)を
UNIQ24238028548781d1-MathJax-329-QINU
定義する場合,
UNIQ24238028548781d1-MathJax-330-QINU
と同値になる.
停留条件
以上のクーン・タッカーの条件下で,
微分可能な写像
UNIQ24238028548781d1-MathJax-331-QINU
が不等式制約UNIQ24238028548781d1-MathJax-332-QINU のもとで
UNIQ24238028548781d1-MathJax-333-QINU で極小(極大)値をとるものとすると,UNIQ24238028548781d1-MathJax-334-QINU次元のラグランジュ乗数ベクトル
UNIQ24238028548781d1-MathJax-335-QINU が存在し,
UNIQ24238028548781d1-MathJax-336-QINU
は,UNIQ24238028548781d1-MathJax-337-QINUで極値条件(停留条件)を充たす.
すなわち
UNIQ24238028548781d1-MathJax-338-QINU
が成りたつ.
さらにUNIQ24238028548781d1-MathJax-339-QINUについては,
UNIQ24238028548781d1-MathJax-340-QINU
が成立つ.
UNIQ24238028548781d1-MathJax-341-QINU
は
UNIQ24238028548781d1-MathJax-342-QINU
と同値になる.