組み合わせ問題
提供: Internet Web School
(版間での差分)
| (間の16版分が非表示) | |||
| 1 行: | 1 行: | ||
ナップサック問題 | ナップサック問題 | ||
| - | 5個の品物<math>1 \sim 5</math>があり,それぞれの重さと値段は表3の通りである.これをナップサックに詰めたいが, | + | 5個の品物<math>1 \sim 5</math>があり,それぞれの重さと値段は表3の通りである.これをナップサックに詰めたいが, |
| - | + | これには10㎏までしか詰め込めない. | |
| - | 品物 | + | |
| - | 重さ | + | 値段の合計が最大となる品物選ぶにはどうすれば良いか. |
| - | 値段 | + | |
| + | |||
| + | |||
| + | {| border="3" class="wikitable" style="text-align: center; " | ||
| + | |品物 | ||
| + | |1 | ||
| + | |2 | ||
| + | |3 | ||
| + | |4 | ||
| + | |5 | ||
| + | |- | ||
| + | |重さ | ||
| + | |5 | ||
| + | |3 | ||
| + | |2 | ||
| + | |4 | ||
| + | |1 | ||
| + | |- | ||
| + | |値段 | ||
| + | |250 | ||
| + | |200 | ||
| + | |150 | ||
| + | |250 | ||
| + | |100 | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | 品物<math>i\ (i=1,2,3,4,5)</math>をナップサックに入れるか入れないかによって | ||
| + | |||
| + | 値<math>1,0</math>を取る変数<math>x_i</math> を導入すると,この問題は | ||
| + | |||
| + | 制約条件 | ||
| + | |||
| + | <math>5x_1+3x_2+2x_3\ +4x_4 + 1x_5 \leq 10</math> | ||
| - | |||
| - | |||
| - | |||
のもとに | のもとに | ||
| - | <math> | + | |
| - | を最大化する問題になる. | + | <math>250x_1+200x_2+150x_3+250x_4 + 100x_5</math> |
| + | |||
| + | を最大化する問題になる. この問題はナップザック問題と呼ばれる組み合わせ最適化問題に属する. | ||
| + | |||
| + | |||
| + | [[ファイル:ナップザック.pdf]]にMicrosoft Excelの ソルバーを用いた解法例を示す. | ||
| + | |||
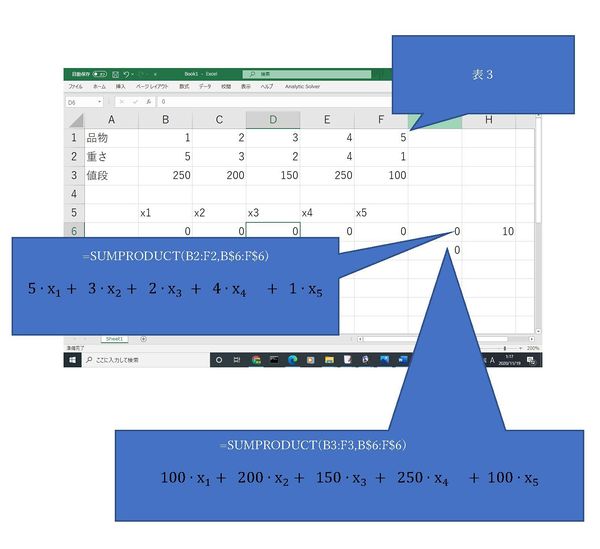
| + | 作成したデータは以下の通りである. | ||
| + | |||
| + | [[ファイル:ナップザック ページ 2.jpg|600px]] | ||
| + | |||
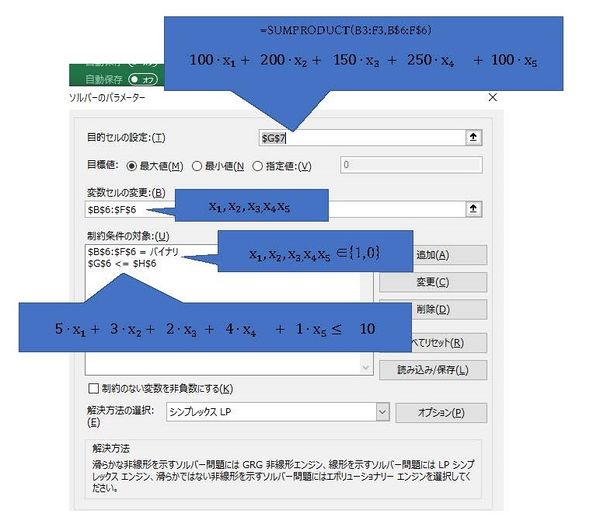
| + | ソルバーのパラメータ 入力は以下の通りである. | ||
| + | |||
| + | |||
| + | [[ファイル:ナップザック ページ 3.jpg|600px]] | ||
| + | |||
| + | |||
| + | ソルバーによる結果は以下の通りである. | ||
| + | |||
| + | [[ファイル:ナップザック ページ 4.jpg|600px]] | ||
| + | |||
| + | |||
| + | |||
| + | 品物2,3,4,5 を詰め込んだときに値段の合計の最大値 700になる. | ||
2020年11月30日 (月) 09:06 時点における最新版
ナップサック問題
5個の品物\(1 \sim 5\)があり,それぞれの重さと値段は表3の通りである.これをナップサックに詰めたいが, これには10㎏までしか詰め込めない.
値段の合計が最大となる品物選ぶにはどうすれば良いか.
| 品物 | 1 | 2 | 3 | 4 | 5 |
| 重さ | 5 | 3 | 2 | 4 | 1 |
| 値段 | 250 | 200 | 150 | 250 | 100 |
品物\(i\ (i=1,2,3,4,5)\)をナップサックに入れるか入れないかによって
値\(1,0\)を取る変数\(x_i\) を導入すると,この問題は
制約条件
\(5x_1+3x_2+2x_3\ +4x_4 + 1x_5 \leq 10\)
のもとに
\(250x_1+200x_2+150x_3+250x_4 + 100x_5\)
を最大化する問題になる. この問題はナップザック問題と呼ばれる組み合わせ最適化問題に属する.
ファイル:ナップザック.pdfにMicrosoft Excelの ソルバーを用いた解法例を示す.
作成したデータは以下の通りである.
ソルバーのパラメータ 入力は以下の通りである.
ソルバーによる結果は以下の通りである.
品物2,3,4,5 を詰め込んだときに値段の合計の最大値 700になる.